From p-Values to Bayes Factors

Most medical papers featuring statistical analysis still utilize a hypothesis testing framework. Data is collected, an analysis is run, a p-value reported, and – if it is found to be below the magic threshold of 0.05 – the finding is declared “(statistically) significant.” The authors then suggest, with varying degrees of explicitness, that their results support their preferred hypothesis, or – in some less modest cases – may go as far as claiming to have found “proof” their preferred hypothesis. Criticism of this methodology is old, and will not be rehashed here. Suffice it to say that the p-value is typically constructed conditional on a strawman “null hypothesis” being true, and as such doesn’t provide direct evidence concerning any specific alternative hypothesis the researchers are actually interested in. What we’re left with is a general desire to say something along the lines of “Based on the data I have collected, I now have more/less reason to believe that my preferred hypothesis is correct.” P-values aside, there exists a measure to express this idea: it is often called the Bayes factor.¹

The Bayes Factor and Its Bound

Let’s start with the basic idea. We can frame the problem of how likely a particular model $M$ is given data $D$ that we have collected by using Bayes theorem:

$$\Pr(M|D) = \frac{\Pr(D|M)\Pr(M)}{\Pr(D)}$$

Suppose you have two competing models as explanations for your data, $M_{1}$ and $M_{2}$. If you want to know if the data favors one model over another, you could simply take that ratio:

$$\frac{\Pr(M_{2}|D)}{\Pr(M_{1}|D)} = \underset{\text{ Bayes Factor}}{\underbrace{\frac{\Pr(D|M_{2})}{\Pr(D|M_{1})}}} \times \underset{\text{Prior Odds}}{\underbrace{\frac{\Pr(M_{2})}{\Pr(M_{1})}}}$$

Which model is in the numerator or denominator can be chosen by convenience. As written above, a larger value of this ratio favors $M_2$ over $M_1$, while small values of the ratio favor $M_1$ over $M_2$.

Substitute in your traditional notation for a null-hypothesis $H_{0}$ and alternative hypothesis $H_{1}$ and we can compare two different Bayes factors, $\text{BF}_{10}$ which compares the alternative hypothesis to the null, or $\text{BF}_{01}$ which compares the null to the the alternative. For illustrative purposes, consider the case of

$$\mathrm{BF}_{10} = \frac{1}{\mathrm{BF}_{01}} = 10$$

We can interpret this to say that the data favor the alternative hypothesis 10 to 1 compared to the null. In other words, bigger values of $ \text{ BF }_{10} $ correspond to greater evidence in favor of $H_{1}$ over $H_{0}$, whereas smaller values of $\text{BF}_{01}$ favor $H_{1}$ over $H_{0}$.

In general, constructing a Bayes factor requires modeling. What we can do without modeling, however, is provide reasonable bounds for the Bayes factor - a minimum bound for $\text{BF}_{01}$ or – equivalently – a maximum bound for $\text{BF}_{10}$. Benjamin and Berger (2019) recommend a particularly simple upper bound for the Bayes factor that can be shown to hold in a wide variety of situations:

$$\text{ BF}_{10} \leq \text{ BFB } = \frac{1}{- ep\log(p)}$$

This approximation is valid for $p < \frac{1}{e} \approx 0.367$.

Adding Bayes Factors to SAS Output

There is an easy way to start adding such Bayes Factor bounds to your existing SAS workflow. Did you know that you can convert any ODS output table to a SAS data set? That way you can access any reported value for later analysis. For our purposes, this means we can access any test statistic or p-value reported by SAS and use them to calculate the appropriate Bayes factor bounds. I’ll show two simple examples.

Let’s say I want to employ a bound for the output of PROC TTEST. I can look up the relevant table name in the SAS/STAT User’s Guide in the “ODS Table Names” section under the PROCs “Details” – in this case, I want to use the table named TTests. I can then save this table to a SAS data set using ods output. To save typing, we’ll use the filename and include statements to utilize the available code for the Getting Started example in TTest:

filename tgs url
  'https://raw.githubusercontent.com/sassoftware/doc-supplement-statug/refs/heads/main/Examples/r-z/ttegs1.sas';
ods output TTests=res; /* this line exports the TTests table to "res" */
%include tgs;

Looking at my new data set, I can see that the p-value is saved to a variable named Probt. I can now use a DATA step to calculate both the BFB and the reciprocal of it, the minimum Bayes factor:

data bayes;
  set res;
  BFB = 1/(-CONSTANT('E')*Probt*Log(Probt));
  BFmin = 1/BFB;
run;
proc print; run;

I’m omitting the data keyword from the PROC PRINT call to keep things concise. This way, it automatically uses the last data set in use. If you run these two code snippets, you’ll get the following table:

This suggests that for our particular example, the most favorable interpretation would favor the alternative hypothesis over the null by a rate of about 5.4-to-1.

Another common source for p-values is regression output. Each parameter estimate is accompanied by a p-value. We can use the same procedure as above to look up the relevant ODS table name and use ODS OUTPUT to save that table for later use:

ods output ParameterEstimates=ParmEst;
proc reg data=sashelp.baseball;
   id name team league;
   model logSalary = nhits nbb yrmajor crhits;
run;

This table contains a little more detail and a pretty large BFB, so I decided to specify which variables I want to print and added a FORMAT to the PRINT call.

data bayes;
  set ParmEst;
  BFB = 1/(-CONSTANT('E')*Probt*Log(Probt));
  BFmin = 1/BFB;
run;

proc print noobs;
  var Variable Label Estimate Probt BF:;
  format BF: COMMA14.2;
run;

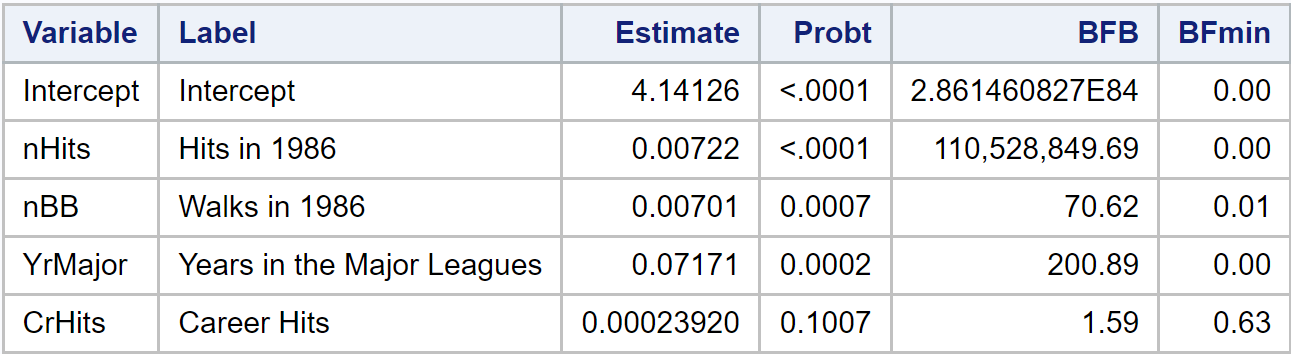
One thing that’s neat to notice here is that the p-value is printed by SAS using a special format. Since user’s are normally not interested in the exact value when it is less than $10^{-4}$ ODS just prints “<.0001.” This doesn’t mean SAS doesn’t calculate the exact p-value as we can see from the data set produced with ODS OUTPUT. It stores the actual numeric value, so the BFB computation can proceed without issues. This is what it looks like:

You can try these code snippets out yourself using SAS OnDemand for Academics or Viya for Learners.

The bound used in this post is one recommendation by Benjamin and Berger (2019) to improve scientific result reporting during this time in which we’re slowly trying to move away from p-values. To learn more about alternative bounds and the conditions in which they hold, I would recommend the very readable overview of the subject of by Held and Ott (2018).

References

Benjamin, D. J., and Berger, J. O. (2019), “Three Recommendations for Improving the Use of p-Values,” The American Statistician, ASA Website, 73, 186–191. https://doi.org/10.1080/00031305.2018.1543135.

Held, L., and Ott, M. (2018), “On p-Values and Bayes Factors,” Annual Review of Statistics and Its Application, Annual Reviews, 5, 393–419. https://doi.org/https://doi.org/10.1146/annurev-statistics-031017-100307.