Lotteries and Pascal's Mugging

Most have heard of Pascal’s wager, but have you heard of the thought experiment known as Pascal’s mugging? The mugging attempts to reframe the essence of the wager argument using only finite values, thereby getting around some standard objections to the wager argument.

Pascal’s Mugging

It appears the term was coined in a blog post by Eliezer Yudkowsky and framed in terms of potential risks posed by AI tasked with solving a problem. Nick Bostrom retells the mugging as a conversation between Pascal and a hypothetical extra-dimensional mugger. The second part of “deal” in the paper is a bit extreme, but the initial part – offering a fixed cost of money now for a low probability payoff tomorrow – reminded me a bit of one of my most frequently discussed posts from 2022 on whether it makes sense to play lottery. To be fair, that was two posts rolled into one – the first part is about how point estimates can be misleading, particularly for skewed distributions, and the second consisted of a mini-benchmark using a simple example calculation to make that point.

The beginning of Bostrom’s version goes something like this: a mugger approaches Pascal and asks for his wallet. Unfortunately, the mugger forgot his weapon so Pascal is disinclined to acquiesce to his request. To still get the wallet, the mugger offers Pascal a deal: give the mugger the wallet anyways, valued at $x$ USD, and the next day the mugger will return and pay Pascal $N x$ USD in return. As the story progresses, $N$ gets larger. We obviously don’t just believe the mugger, so there is some (small) probability $p$ that the mugger will return with the promised reward. The idea behind the experiment is that if $N$ grows sufficiently large then for any non-zero $p$ the expected value of paying the mugger becomes positive. It then veers off talking about other utility issues to make the payout better, but this early part of the conversation is essentially equivalent to a lottery game. Pay for the ticket now in the hopes that come game night the right numbers show up and you’re rich.

As stated, it would appear that it is reasonable for Pascal to pay the mugger and – for a sufficiently large jackpot – to play the lottery, even though intuitively it strikes us as the “wrong answer” given the low probability of winning. This got me thinking: can we steelman the case for playing the lottery by ignoring the magnitude of the win?

Let’s Crunch Some Numbers

If we ignore the question of the exact magnitude of the lottery win, we can divide the event space into three possibilities – we are either worse off (cost of buying ticket), win back the ticket cost only, or win more money than the ticket cost so that we have a net gain from playing. Working off of the published odds again as a shortcut, we wind up with the following probabilities:

$$ \begin{cases} Pr(\text{loss}) = 24/25 \\
Pr(\text{even}) = 1/38 \\
Pr(\text{gain}) = 13/950 \end{cases} $$

I’ll postulate that people don’t really care about just breaking even on the ticket, so from a decision point of view it probably makes sense to reduce this to a binomial problem: I either win or loose on each ticket, where loosing includes the case of breaking even. People usually buy a handful of tickets, call it $n$. So now I can write a random variable representing my number of winning tickets as

$$ X \sim \mathrm{Bin}\left(n, \frac{13}{950} \right). $$

We already showed that within any reasonable lifetime, there is a vanishingly small chance you’ll become rich from playing the lottery. To steelman, we’ll say that the utility of playing the lottery comes not from the money won but from the fun of playing.

I’ll start by asserting that winning is more fun than loosing. So how often can we loose and still have fun? We definitely don’t want to always loose, so $x>0$ is required. Winning more often than we loose is unlikely by design of the lottery so that can be our upper bound. Our realistic expectation should then be something like $0 < x \leq \left \lfloor{n/2}\right \rfloor$. If $x$ is in this window, I’ll call it a “Good Game” of lottery.

Realistically, you’re not going to buy 100+ lottery tickets. Let’s say an average person likely wouldn’t buy more than 20 tickets, which still feels like plenty. So how likely is it you’ll have a good game, given as a function of the number of lottery tickets purchased? Let’s do a quick DATA step and find out.

data lottery;
  p=13/950;

  do N=2 to 20;
    gg=cdf('Binomial', floor(N/2), p, N) - cdf('Binomial', 0, p, N);
    output;
  end;
; run;

proc sgplot data=lottery;
  scatter x=N y=gg;
  xaxis label='Number of Tickets';
  yaxis label='Probability of a Good Game';
run;

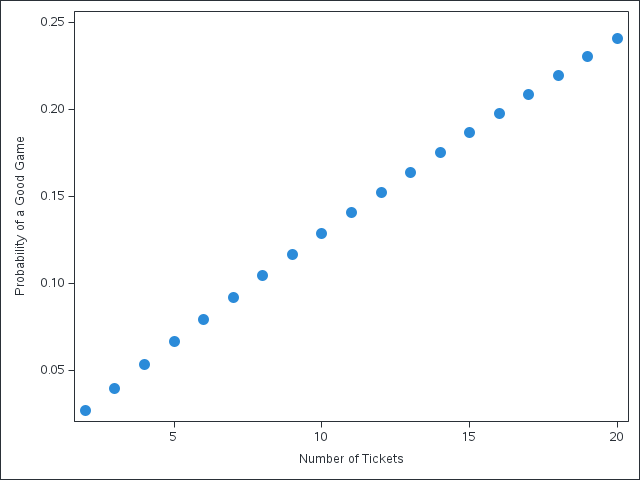
So in the best case scenario, where we buy 20 tickets, we only have a chance of approximately 0.24 of having a good time. In other words, even with the generous assumption you’d be happy to loose 19 games if you win 1 you’d still be disappointed most of the time. Given my experience, I’d say many people will probably purchase fewer than 20 tickets. Perhaps 2 to 6. In such cases, you’re still bound to be disappointed. I’d say even with this steelmanning, it doesn’t make sense. Instead of buying a lottery ticket, perhaps buy a coffee and a donut for similar cost but with a guaranteed happiness payoff.